Waarom heeft Denemarken zoveel minder “oversterfte” tijdens de coronacrisis dan België
2020 toont grote pieken in de overlijdens, terwijl er normaal elk jaar in verhouding minder mensen sterven
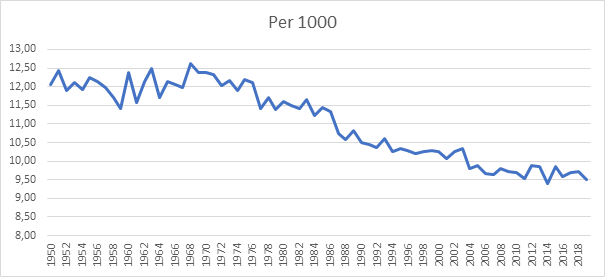
Al jaren daalt de ratio van het aantal overlijdens per duizend inwoners in België. Dat komt gewoon omdat mensen steeds langer leven door een goede gezondheidszorg. Maar die dalende tendens zwakt inderdaad de laatste jaren wat af. Hoe komt dat? Dat komt onder meer doordat de generatie babyboomers langzaam begint te sterven. Die babyboomers zijn met velen en dus zijn er ook wat vaker overlijdens. In onderstaande grafiek wordt de evolutie van het aantal overlijdens per 1000 inwoners weergegeven:
Dr. Els Ooms vindt dat onder meer dit effect wordt onderschat. Maar zonder dat we grote statistiek moeten bovenhalen, kunnen we al meteen zien dat het hier om appelen en citroenen gaat. De sterftecijfers kan iedereen gewoon opzoeken op euromomo.eu. Daar vind je onder meer deze grafiek die een overzicht geeft van de overlijdens in België vanaf eind 2015. Voor alle duidelijkheid: het gaat daarbij over àlle overlijdens, wat de doodsoorzaak ook zij. Ook wie omkwam bij een brand wordt meegeteld.
Overlijdenspieken vallen samen met pieken in coronabesmettingen, zelfs als de parameters verhoogd worden
Je ziet onmiddellijk dat er grote sterftepieken zijn in maart-april en in oktober-november van 2020. Die pieken in het aantal overlijdens vallen samen met pieken in coronabesmettingen. De lichtblauwe strook geeft aan wat een “normale” sterfte zou kunnen zijn. Als de pieken over de rode lijn gaan, is er “oversterfte”, meer overlijdens dan verwacht dus. Oversterfte komt ook in andere jaren voor. Bijvoorbeeld door een zware griepepidemie in 2018. Maar iedereen kan zien dat de pieken in 2020 veel groter zijn.
Dr. Els Ooms zegt dat de rode lijn wat hoger zou moeten liggen, onder meer door de babyboomers die sterven. Maar daarmee redeneer je de pieken niet weg. Het is niet alsof alle babyboomers gezamenlijk besloten hebben om in maart en april te sterven. De meer voor de hand liggende verklaring is toch dat die overlijdenspieken iets te maken hebben met de piek in coronabesmettingen op dat moment. Dat de rode lijn misschien ook wat hoger kan, verandert niets aan het algemene beeld.
De berekening van Sciensano voor een “normaal’ sterftecijfer” is niet afwijkend of verrassend
Sciensano berekent dat een “normaal” aantal overlijdens voor 2020 108.000 zou zijn. Dat is dus de stippellijn in de lichtblauwe zone. Sterke afwijkingen van die stippellijn is over- of ondersterfte.
Maar Els Ooms zegt dus dat die lichtblauwe zone en rode lijn hoger zouden moeten liggen. Daarvoor gebruikt ze allerlei methodes die het verwachte, normale sterftecijfer steeds hoger doen uitkomen. Uiteindelijk zou zelfs een verwacht sterftecijfer van 141.640 overlijdens voor 2020 als “normaal” kunnen doorgaan.
Dat is absurd want het jaar voordien, in 2019, zijn er maar 108.745 mensen gestorven. Dat is het échte cijfer, geen schatting. Nu is het best mogelijk om geleidelijk evoluties zoals het sterven van de babyboomers of de aangroei van de bevolking wat anders in te schatten, maar het moet toch al heel vreemd lopen als er - zonder impact van corona - plots vele duizenden doden extra zouden vallen. (Van 108.745 op één jaar naar bijvoorbeeld 141.640 zonder corona.)
De échte sterftecijfers, geen berekeningen, staan gewoon op de site van Statbel. Dit zijn ze:
2017 109.629
2018 110.645
2019 108.745
2020 127.134
Het valt meteen op dat 2020 wel degelijk een uitzonderlijk jaar is. Els Ooms blijft parameters verleggen en herschatten tot ze uitkomt bij een “normaal” sterftecijfer in 2020 dat vele duizenden boven dat van vorige jaren ligt. Dat is zeer onaannemelijk. Bevolkingscijfers maken niet dat soort plotse sprongen, tenzij er iets speciaals aan de hand is, zoals bijvoorbeeld corona.
Maar stel nu dat we in zoverre meegaan dat de daling van het aantal overlijdens per duizend in 2020 vanzelf zou zijn gestopt. Wat krijgen we dan?
Ook bij een sterfteratio die niet meer daalt, blijft er in 2020 oversterfte
Sciensano gaat bij haar berekening inderdaad uit van een langzaam dalende sterfteratio. Laat ons dan eens kijken wat er gebeurt als we dat niet doen. Wat als we ervan uitgaan dat in 2020 de daling van de Belgische “normale” sterfteratio volledig zou zijn gestopt?
Ook als we als basis 2019 nemen, is er een grote oversterfte
Als 2020 helemaal geen “normale” daling in de sterfteratio had, dan zou de sterfteratio dus ongeveer gelijk moeten zijn aan dat van 2019. We bekijken dus welk aandeel van de bevolking in 2019 is gestorven zonder corona. De cijfers vindt men opnieuw bij Statbel. Met het bevolkingsaantal en het aantal overlijdens kan men de sterfteratio berekenen. Dat cijfer is afgerond 9,51 per duizend mensen. De sterfteratio daalt al vele jaren, maar we gaan er nu dus vanuit dat er geen daling is. We nemen voor 2020 dus hetzelfde cijfer als voor 2019.
Akkoord, dit houdt geen rekening met andere verschillen die er tussen 2019 en 2020 kunnen zijn : vergrijzing, griep en dergelijke. Het blijft een schatting, maar het geeft ons wel een idee over de vraag of de berekening van Sciensano nu al dan niet wereldvreemd is. Op basis van de sterfteratio van 2019 komen we uit op een “normaal” aantal overlijdens van 109.328 in 2020. Een hoger getal dan dat van Sciensano. Maar de oversterfte is dan nog altijd 16 procent. Geen wezenlijk verschil dus.
Ook drie voorgaande jaren als basis levert een grote oversterfte op
Maar misschien was 2019 toevallig een wat “makker” jaar met relatief weinig overlijdens. Goed, laat ons dan de gemiddelde sterfteratio (afgerond 9.64) nemen van de voorbije drie jaren. Dan komen we nog op een hoger getal uit. Dan zouden 110.796 overlijdens “normaal” zijn geweest in 2020. In werkelijkheid zijn er in 2020 127.134 mensen overleden. Nog altijd een oversterfte van bijna 15 procent.
Wat je met dat soort oefeningen leert, is dat ook statistiek natuurlijk ook wordt beïnvloed door keuzes en inschattingen die je maakt. Niemand ontkent dat. Maar de conclusie blijft onvermijdelijk: in 2020 zijn er veel meer mensen gestorven dan normaal.
Herberekenen voor de hittegolf zorgt niet voor een ondersterfte
Ook hittegolven kunnen soms zorgen voor een kleine piek in de overlijdens. Maar dat verandert niet veel aan het fundamentele beeld. Als we het totale aantal echte overlijdens in 2020 verminderen met het aantal overlijdens door de hittegolf (volgens Sciensano 1.460) komen we uit bij 125.674 overlijdens, nog altijd 16% meer dan de 108.000 die door Sciensano als “normaal”’ werden geschat.
Dr. Ooms komt via de hittegolf en haar andere berekeningen zelfs uit bij een ondersterfte in 2020. (Er zouden dus minder mensen overleden zijn dan je normaal kon verwachten.) Dat is toch wel kras. We geven nog even een grafiek mee van Statbel die het échte aantal overlijdens (geen schattingen) van de verschillende jaren gewoon bovenop elkaar plaatst. De rode lijn van 2020 toont toch echt wel aan dat vorig jaar een heel uitzonderlijk jaar was inzake overlijdens. Je ziet ook dat de overlijdens het hoogste waren in maanden waarin er niet meteen een hittegolf was.
Mandelbrot, Simpson en de statistische trukendoos
Om de geloofwaardigheid van de cijfers en statistieken van Sciensano en Statbel onderuit te halen sleurt dr. Ooms er de fractalen van Mandelbrot en de paradox van Simpson bij. Wat is dat eigenlijk?
Benoît Mandelbrot: doden zijn geen zandkorrels aan de kust
Benoît Mandelbrot is een wiskundige die vooral bekend is voor zijn werk rond de fractaaltheorie. Dit is een fascinerende tak in de wiskunde over geometrische figuren die bij uitvergroting zichzelf steeds herhalen in kleinere vorm. Dr. Ooms beschrijft bijvoorbeeld dat je de grens van een land nooit exact kan meten. Je kan grofweg zeggen dat een kustlijn 100 km lang is. Maar als je meer in detail rekening houdt met bochten en oneffenheden, dan wordt het gemeten resultaat groter. Als je verder gaat en rekening houdt met kleinere onregelmatigheden dan wordt het meetresultaat nog groter. En zo verder: uiteindelijk moet je zelfs de ronding van elke zandkorrel afzonderlijk meten, en het resultaat wordt dan nog veel groter. Uiteindelijk gaat het erover hoe je de kustlijn precies definieert.
Hoewel boeiend, kan men deze theorie niet zomaar overal toepassen. Je moet er niet mee aankomen bij een schrijnwerker die ramen en deuren gaat installeren of een metselaar die een muurtje bouwt. Bij het tellen van doden door Statbel gaat die theorie ook niet op. Iemand is ofwel levend of dood, en uitvergroten heeft geen enkel effect op het meetresultaat. Er zijn geen “inkepingen in de kust”. Levend of dood, er is geen tussenweg. Bij oversterftecijfers maakt het ook niet uit wat de doodsoorzaak was. Corona of een auto-ongeval, iedereen wordt meegeteld. En dan blijken er in 2020 gewoon veel meer mensen overleden, zoals op de bovenstaande grafiek van Euromomo te zien is.
De paradox van E.H. Simpson: een wel heel verre omweg
Dr. Ooms gaat echter met het ‘masseren’ van de cijfers en beroept zich daarvoor op de Simpson paradox. Die waarschuwt voor het gevaar voor tegenstrijdige conclusies door het segmenteren van de groep die men statistisch onderzoekt. Een voorbeeld: mijn vrouw en ik willen coronaproof op restaurant, maar we kunnen geen overeenstemming bereiken. Ik kies restaurant A, mijn vrouw wil naar restaurant B. Ik voer als argumentatie aan: uit de beoordelingen op sociale media blijkt dat vooral vrouwen een voorkeur hebben voor A. Mijn vrouw voert aan dat restaurant B in totaal veel meer positieve reacties heeft dan restaurant A. Mijn vrouw en ik segmenteren de reviewers van de restaurants op een andere manier. Wie heeft gelijk?
Dr. Ooms probeert op het geschatte aantal van 108.000 overlijdens van Sciensano uit te komen door een aantal gecompliceerde berekeningen over 3 jaar, 5 jaar, 10 jaar, 15 jaar en zelfs 29 jaar. Een soort Simpson segmentatie. Het bekomen cijfer is uiteraard steeds verschillend en dus volgens de Simpson paradox vatbaar voor tegenstrijdigheden. Om de zaak nog verder te compliceren en te segmenteren geeft dr. Ooms telkens de uitsplitsing per leeftijdsgroep. Zeer interessant, maar niet relevant en zelfs een overkill om het cijfer 108.000 van Sciensano te beoordelen. Die omwegen zijn niet nodig omdat de leeftijdspiramide de laatste jaren niet bruusk is veranderd en ook de verhouding van het aantal vrouwen/mannen blijft zeer stabiel. De samenstelling van de bevolking verandert zeer langzaam, we kunnen dus de opeenvolgende jaren wel degelijk met elkaar vergelijken.
Het percentage berekend door Sciensano is niet verrassend of afwijkend
Daar stopt het niet, er volgen nog een rist manieren om geschatte sterfte en oversterfte te berekenen, waarbij de ongeduldige lezer al snel de draad verliest en misschien al snel overgaat naar de conclusies van dr. Ooms. Die komen erop neer dat de oversterfte van 16%, zoals berekend door Statbel en ruim gepubliceerd in pers, schromelijk overdreven zou zijn.
Maar om het cijfer van Sciensano snel te beoordelen volstaat de methode die we hoger hebben toegepast. De 108.000 liggen in lijn met de echte sterftecijfers van de afgelopen jaren en zijn niet verrassend als we bij wijze van snelle steekproef de sterfteratio’s van de vorige jaren toepassen op 2020. De analyses van Els Ooms leveren soms juist wel sterk afwijkende cijfers op.
Verlies van potentiële levensjaren
Tenslotte berekent dr. Ooms ook het ‘verlies van potentiële levensjaren’. Mensen ouder dan 75 jaar worden arbitrair niet meegeteld in die berekening, elk extra jaar dat deze ouderen leven wordt aanzien als ‘gewonnen’. Voor elke persoon die overlijdt vóór de leeftijd van 75 jaar, wordt berekend hoeveel jaren die persoon gemiddeld nog zou geleefd kunnen hebben. Die verloren jaren worden dan opgeteld en omgezet in een aantal mensenlevens. Deze manier van rekenen komt een beetje gruwelijk en koud berekend over, maar wordt veel gebruikt bij de analyse van de ernst van ziekten of rampen, waarbij bijvoorbeeld berekend wordt hoeveel levensjaren kanker kost aan een totale bevolking.
Zodoende herleidt dr. Ooms het aantal vroegtijdige overlijdens in 2020 tot ongeveer 677 ‘doden’. Dr Ooms komt zelfs tot de conclusie dat er in 2020 een winst is van 336 mensenlevens in vergelijking met de voorgaande 10 jaar. Een ondersterfte dus in plaats van een oversterfte. Dit geeft uiteraard een vertekend resultaat, want net de leeftijdscategorie die meest kwetsbaar is voor corona - boven de 75 - wordt niet meegeteld, Hoewel dr. Ooms pleit voor meer aandacht en inspraak voor de ouderen, worden de 75-plussers niet meegerekend om toch maar te beargumenteren dat de coronamaatregelen overdreven zijn.
Els Ooms spreekt wel heel dure woorden
Dr. Els Ooms zegt in de titel van haar werkstuk dat de wetenschap “in haar blote kont staat”. Ze spreekt zelfs over “foefelen met data’ terwijl ze zelf toegeeft dat ze niet precies weet hoe Sciensano haar cijfer heeft berekend. Ze noemt de cijfers ook “bedrieglijk”. De CEO’s van mediabedrijven zouden aan dat bedrog meedoen uit drang om winst te maken. Dat zijn allemaal vrij zware beschuldigingen.
Nu is het natuurlijk altijd mogelijk om te discussiëren over aannames in de statistiek. Maar de polemische toon van het artikel is toch wat vreemd voor een werkstuk met wetenschappelijke pretentie, zelfs als het gaat om een stuk voor het grote publiek.
Conclusie: trukendozen veranderen de werkelijkheid niet
De berekening van Sciensano voor wat een “normale” sterfte zou geweest zijn in 2020 is niet vreemd of opvallend als we kijken naar de cijfers van de jaren ervoor.
Hoe men de statistische trukendoos ook laat draaien, de meest voor de hand liggende conclusie blijft dat er in 2020 opvallend meer mensen zijn gestorven dan de voorgaande jaren. De échte sterftecijfers (geen berekeningen) zijn wat ze zijn: 127.134 overlijdens in 2020 tegenover 108.745 in 2019.
De pieken in de overlijdens van 2020 (maart-april, oktober-november) vallen ook samen met het moment dat onze ziekenhuizen volliepen met mensen met ademhalingsproblemen. Alleen al daarom is het niet vreemd om te denken dat de onontkenbare oversterfte in 2020 echt wel verband houdt met de corona-epidemie.